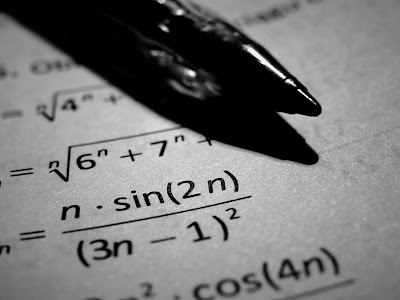Articles

Dernier Article

Les sommes : la sommation par paquets

Le principe de la sommation par paquet est de séparer une somme initiale en une somme de sommes (je sais, c'est bizarre !). Par exemple, on peut séparer une somme banale avec d'un côté les nombres pairs et de l'autre les nombres impairs. Cela peut-être d'une aide bienvenue en trigonométrie ou avec $(-1)^k$. Exemple : $$\sum_{k=0}^{2n} k = \sum_{\lceil{k=\frac{0}{2}}\rceil}^{\lfloor{\frac{2n}{2}}\rfloor} 2k + \sum_{\lceil{k=\frac{0}{2}}\rceil}^{\lfloor{\frac{2n-1}{2}}\rfloor} 2k + 1 = \sum_{k=0}^{n} 2k + \sum_{k=0}^{n-1} 2k + 1$$ Le processus pas à pas : Je commence par construire le membre des nombres impairs en soustrayant -1 à droite (j'ajoute donc +1 à gauche). $$\sum_{k=-1}^{2n-1} k + 1$$ Puis, je remplace k par 2k, et donc je divise -1 et 2n par 2. $$\sum_{k=\frac{-1}{2}}^{\frac{2n-1}{2}} 2k + 1$$ Et je termine par les arrondis supérieurs et inférieurs : $$\sum_{k=\lceil{\frac{-1}{2}}\rceil}^{\lfloor{\frac{2n-1}{2}}\rfloor} 2k + 1$$ Je pa
Continuer la lecture

Les démonstrations par récurrence

Image
Le raisonnement par récurrence (avec deux r s'il vous plait) est une méthode de démonstration d'une conjecture, c'est à dire d'une supposition. Une fois la récurrence terminée et la conjecture prouvée, elle deviendra une assertion vraie (sachant qu'une assertion peut-être vraie ou fausse mais pas les deux, c'est le principe dit du "tiers-exclu". Toutefois, les différentes définitions des termes de logique mathématique peuvent parfois différer légèrement et sont sujettes à débat. Le "tiers-exclu" en logique mathématique correspond à la disjonction des propositions p / non p. En clair, sur les deux propositions, l'une des deux est forcément vraie (si p est vraie, alors p est vraie et si p est fausse, non p est vraie...) Si la proposition est vraie à un certain point fixe (ex: n= 1) et, sachant qu'elle est vraie pour un n quelconque elle est aussi vraie pour le n suivant, alors la proposition est vraie pour tous les n plus g
Continuer la lecture

Déterminer la racine carrée d'un complexe

Un nombre complexe, communément noté $z$, s'écrit dans sa forme algébrique $z = a + ib$ ; avec a et b des réels. Aujourd'hui, nous allons voir comment déterminer la racine d'un nombre complexe. Pour cela, il suffit de poser : $$\omega^2 = z$$ Avec $$\omega$$ un nombre complexe tel que $$\omega = x + iy$$. Le but sera de déterminer x et y en fonction de a et b pour trouver $$\omega$$. Tout d'abord, développons $$\omega^2$$. $$(x+iy)^2 = x^2 + (iy)^2 + 2xyi = (x^2 - y^2) + i*(2xy)$$ Nous savons que deux nombres complexes sont égaux si et seulement si leurs parties réelles et imaginaires sont égales. Nous avons donc ici l'égalité : $$(x^2 - y^2) + i*(2xy) = a + ib$$ Et nous en déduisons le couple suivants : $$x^2 - y^2 = a $$ $$2xy = b$$ Comme je l'ai dit plus tôt, nous cherchons à exprimer x et y séparément et en fonction de a et b. Pour cela, il nous faut une troisième égalité. Comme nous savons que deux nombres complexes égaux ont des modu
Continuer la lecture

Singularité technologique : La question de la fin de l’humanité

Image
La singularité technologique est une théorie selon laquelle à un moment donné, le progrès technologique et technique sera tellement rapide qu’il n’y aura plus de progrès à faire, autrement dit nous (ou quelque chose comme on le verra plus tard) aurions une compréhension absolue ou minimum du monde. Même si cela ressemble plus à un scenario de science-fiction asimovien se déroulant à l’an 10 000, cette théorie est sérieusement étudiée par certains scientifiques qui osent parfois affirmer que la singularité se produira au 21ème siècle. Le but de cet article est de faire découvrir le concept de la singularité et de poser les questions liées à cette théorie. Je ne considérerais donc pas les arguments réfutant la possibilité de cet évènement aussi valables qu’ils sont. Singularité : Comment en arrive-t-on là ? On s’accorde à le dire, le progrès technologique explose. Et on dit souvent que personne n’aurait pu prédire un an en arrière où on en serait aujourd’hui. Et s
Continuer la lecture

Démonstration de dérivées #1

Image
Les dérivées forment un outil mathématiques formidable dès lors qu'il s'agit d'étudier des fonctions. Ainsi, par l'étude du signe d'une dérivée nous sommes en mesure de dire que la fonction est croissante ou décroissante. Mais cela va au-delà : les équations différentielles, très employées en physique et biologie (équations de Lotka Volterra par exemple) nous font chercher un couple formé par une fonction et sa dérivée (première, seconde...). Pour déterminer le nombre dérivé d 'une fonction en un point, on utilise la limite du taux d’accroissement en ce point . La formule générale est :  $\displaystyle \lim_{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}$ Fonction étudiée :  $f(x)=x^2$ $\displaystyle \lim_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}$ $\displaystyle \lim_{h \rightarrow 0} \frac{(x+h)^2-x^2}{h}$ $\displaystyle \lim_{h \rightarrow 0} \frac{x^2 +2xh +h^2 -x^2}{h}$ $\displaystyle \lim_{h \rightarrow 0} \frac{h(2x +h)}{h}$ $\displaystyle \
Continuer la lecture

Solving common core maths problems #3

Image
Common core mathematics are essentially fun and tricky. Not necesserly in that order. Let's solve some of these maths problems that became meme over the internet. In this serie, you will find a few ways to improve yourself at solving common core maths. Because, if you think a bit to the last problem you find on your favorite social network, it was kind of tricky (and tricky is an euphemism). However, if you have the feeling common core problems are tricky, hard or just weird, that's only because they are based on simple and very easy problems. These problems are then complicated to make them looking hard. But they are not - and if you can't solve one of them within 2 minutes, you are not dumb. Click here t o see the previous problem . The Problem  And so... Where to start? A solution Let's write equations instead of th ese colo red squares . Blue = x ; Orange = y ; Green = z ; Yellow = t $x-y=9$ $y+z=2$   $t-z = 14$ $x + t
Continuer la lecture