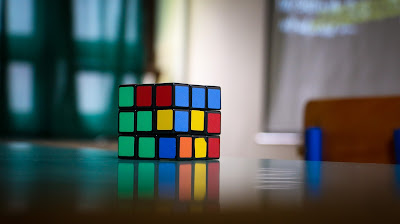Solving common core maths problems #3


Common core mathematics are essentially fun and tricky. Not necesserly in that order. Let's solve some of these maths problems that became meme over the internet. In this serie, you will find a few ways to improve yourself at solving common core maths. Because, if you think a bit to the last problem you find on your favorite social network, it was kind of tricky (and tricky is an euphemism).

However, if you have the feeling common core problems are tricky, hard or just weird, that's only because they are based on simple and very easy problems. These problems are then complicated to make them looking hard. But they are not - and if you can't solve one of them within 2 minutes, you are not dumb.

Click here to see the previous problem.

The Problem 

And so... Where to start?

 A solution

 Let's write equations instead of these colored squares.

Blue = x ; Orange = y ; Green = z ; Yellow = t

 $x-y=9$

$y+z=2$
 
$t-z = 14$

 $x + t=12$

 The problem is half solved! We now have four equations with four variable. Let's solve this! (and use matrix, because it's fun).

A will be the "variables coefficients" matrix. B will be the "variables" matrix and C will be the solution matrix.

$A*B = C$

$B = A^{-1} * C$ 
Let's rearrange the variables in order to get a square matrix (4 variables means 4 rows & 4 columns)

NB : in this particular case, the A matrix is inversible. In the case A wasn't inversible ($A^{-1}$ doesn't exist) we would have used a regular way to solve the equations system.

$1x - 1y + 0z + 0t =9$

$0x +1y + 1z + 0t =2$

$0x + 0y - 1z + 1t = 14$

$1x + 0y + 0z + 1t =12$

$\begin{bmatrix}1&-1&0&0\\0&1&1&0\\0&0&-1&1\\1&0&0&1\end{bmatrix}$ * $\begin{bmatrix}x\\y\\z\\t\end{bmatrix}$ = $\begin{bmatrix}9\\2\\14\\12\end{bmatrix}$

We found our solutions are :

$\begin{bmatrix}x\\y\\z\\t\end{bmatrix}$ = $\begin{bmatrix}7\\16\\-2\\21\end{bmatrix}$

 Problem solved! 
Clément
Fondateur du blog Point Carré et philognoseur. Ecrit sur des sujets variés, essentiellement pour ses études et parfois juste par plaisir !

Articles populaires

Les sommes : la sommation par paquets

Le principe de la sommation par paquet est de séparer une somme initiale en une somme de sommes (je sais, c'est bizarre !). Par exemple, on peut séparer une somme banale avec d'un côté les nombres pairs et de l'autre les nombres impairs. Cela peut-être d'une aide bienvenue en trigonométrie ou avec $(-1)^k$. Exemple : $$\sum_{k=0}^{2n} k = \sum_{\lceil{k=\frac{0}{2}}\rceil}^{\lfloor{\frac{2n}{2}}\rfloor} 2k + \sum_{\lceil{k=\frac{0}{2}}\rceil}^{\lfloor{\frac{2n-1}{2}}\rfloor} 2k + 1 = \sum_{k=0}^{n} 2k + \sum_{k=0}^{n-1} 2k + 1$$ Le processus pas à pas : Je commence par construire le membre des nombres impairs en soustrayant -1 à droite (j'ajoute donc +1 à gauche). $$\sum_{k=-1}^{2n-1} k + 1$$ Puis, je remplace k par 2k, et donc je divise -1 et 2n par 2. $$\sum_{k=\frac{-1}{2}}^{\frac{2n-1}{2}} 2k + 1$$ Et je termine par les arrondis supérieurs et inférieurs : $$\sum_{k=\lceil{\frac{-1}{2}}\rceil}^{\lfloor{\frac{2n-1}{2}}\rfloor} 2k + 1$$ Je pa
Continuer la lecture

Mo et Mb, différences et conséquences

Image
Vous avez probablement déjà remarqué que l'on parlait tantôt de MégaBits (Mb) et tant ôt de MégaOctet (Mo). Pourquoi cette différence et quelles sont les conséquences pour nous, usager d'internet ? Il suffit pour cela de comprendre la différence entre Byte et Bit. En effet, Mb = Mégabit et MB = Mégabyte. Un bit est la plus petite unité du système informatique (celle qui prend alternativement la valeur 0 ou 1 - le ou est important car dans les ordinateurs quantique, il se transforme en et mais c'est une autre histoire...). Une byte vaut 8 bits. Et un byte vaut également un octet. Pour faire simple, quand il y a un B majuscule, on parle de Byte et quand il y a un b minuscule on parle de bit. Par conséquent, il y a 8 fois moins de "quantité de donnée" dans un Mo que dans un Mb. Or, les Mb sont utilisés pour définir le débit internet. Ainsi, la vitesse maximum d'une carte réseau "standard" (id est équipant la majorité des terminaux
Continuer la lecture

Les démonstrations par récurrence

Image
Le raisonnement par récurrence (avec deux r s'il vous plait) est une méthode de démonstration d'une conjecture, c'est à dire d'une supposition. Une fois la récurrence terminée et la conjecture prouvée, elle deviendra une assertion vraie (sachant qu'une assertion peut-être vraie ou fausse mais pas les deux, c'est le principe dit du "tiers-exclu". Toutefois, les différentes définitions des termes de logique mathématique peuvent parfois différer légèrement et sont sujettes à débat. Le "tiers-exclu" en logique mathématique correspond à la disjonction des propositions p / non p. En clair, sur les deux propositions, l'une des deux est forcément vraie (si p est vraie, alors p est vraie et si p est fausse, non p est vraie...) Si la proposition est vraie à un certain point fixe (ex: n= 1) et, sachant qu'elle est vraie pour un n quelconque elle est aussi vraie pour le n suivant, alors la proposition est vraie pour tous les n plus g
Continuer la lecture